La tecnica di Van der Pauw: misure di resistività e mobilità dei portatori
La tecnica utilizzata per ricavare i valori di resistività e mobilità dei portatori è detta di Van der Pauw, dal nome del suo ideatore.
Essa consente di ricavare, per un campione di spessore uniforme, la resistività di strato prescindendo del tutto dai parametri geometrici del campione; con la stessa disposizione dei contatti è inoltre in grado di effettuare una misura di effetto Hall per ricavare la mobilità.
La misura di resistività di strato è basata su una trasformazione conforme del dominio costituito dal campione in un semipiano, la cui origine è l’immagine del bordo del campione. Per ottenere risultati accurati è necessario disporre di contatti molto piccoli rispetto alle dimensioni del campione e situati sui bordi di questo.
In figura 1.1 è rappresentato un esempio di disposizione dei contatti, insieme a un generatore di corrente e un misuratore di tensione in una delle configurazioni necessarie alla misura.
La tecnica è basata sulla misura della caduta di tensione su due contatti adiacenti in seguito al passaggio di corrente fra altri due.
Indichiamo con
![]() =
=![]() /
/![]() (2.11)
(2.11)
Il rapporto tra la tensione che si stabilisce tra i contatti k e I dovuta alla corrente che scorre tra i contatti i e j; Van der Pauw ha dimostrato che in queste condizioni la resistività di strato del campione vale:
![]() (2.12)
(2.12)
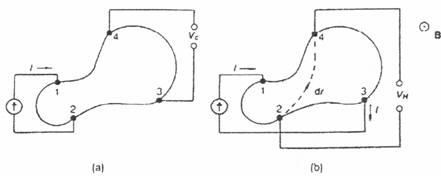
Figura 2.1. Una forma arbitraria per le misure con il metodo di Van Der Pauw.
(a) Misura di resistività. (b) Effetto Hall.
dove f è un
fattore correttivo legato al rapporto tra
![]() e
e
![]() definito
da un’equazione implicita.
definito
da un’equazione implicita.
Tale equazione è stata risolta numericamente con il metodo di Newton ed il fattore correttivo così ottenuto è stato utilizzato nel programma realizzato per le misure.
Un miglioramento della tecnica che permette di escludere errori dovuti alla geometria del campione consiste nel mediare le resistenze ottenute scambiando tensione e corrente e invertendo il senso della corrente; è stato inoltre ricavato un ulteriore fattore di correzione per tenere conto della dimensione finita dei contatti.
In particolare, In questo caso la resistività è data da:
![]() (2.12a)
(2.12a)
Dove
![]() e
e
![]() sono
dei fattori correttivi.
sono
dei fattori correttivi.
Per la misura della tensione di Hall, che permette di ricavare concentrazione di portatori e mobilità, si usa la configurazione rappresentata in fig. 1.1b.
Trascurando gli effetti magnetoresistivi e di ordine superiore,la relazione tra campo elettrico, campo di induzione magnetica e densità di corrente in un semiconduttore isotropo è:
E
=
![]() J +
J + ![]()
![]() (J
(J![]() B) (2.13)
B) (2.13)
Dove
![]() è detta mobilità di Hall.
è detta mobilità di Hall.
La differenza di potenziale tra i contatti 2 e 4 (fig. 3.12b) vale, in assenza di campo magnetico
![]() (2.14)
(2.14)
In presenza di un campo di induzione magnetica B si ha
![]() (2.15)
(2.15)
Se trascuriamo la magnetoresistività, nell’ipotesi di contatti puntiformi, il campo magnetico non influenza la corrente, quindi J=J* e la tensione di Hall tra i contatti 2 e 4 vale
![]() (2.16)
(2.16)
Se l’induzione magnetica è uniforme e ortogonale al flusso della corrente, la 15) diventa:
![]() (2.17)
(2.17)
da cui è possibile
ricavare il valore della mobilità di Hall, nota la resistività di strato.
La mobilità di Hall è legata alla mobilità di trascinamento dal parametro
![]() ,
che dipende, oltre
che dalla struttura delle bande energetiche, anche dai fenomeni di
scattering; esso, quindi, non è determinato unicamente dal materiale ma
dipende, per esempio, dal drogaggio.
,
che dipende, oltre
che dalla struttura delle bande energetiche, anche dai fenomeni di
scattering; esso, quindi, non è determinato unicamente dal materiale ma
dipende, per esempio, dal drogaggio.
Data l’impossibilità di conoscere l’esatto valore di r e considerando che nei casi noti in letteratura per il fosfuro d’indio tale parametro non si discosta troppo dall’unità, assumiamo r = l.
Integrando la (2.6) membro a membro su tutto lo spessore e ricordando le (2.7) e (2.8) si ottiene:
![]() =
=![]() (2.18)
(2.18)
Da cui è possibile ricavare la concentrazione di portatori per unità di superficie, e misurare quindi tutte le caratteristiche elettriche di nostro interesse.